2012-03-20 11:30:54
More Loop Racing
Here are some perhaps interesting benchmarks involving the simple loop:
( c ) ✂
where sum is a double and i is an integer. I had seen some old slides about compiling this on PPC machines that indicated that using a "ghost" double variable in the loop would triple the speed of the loop, so I had to try that on my Xeon. It goes something like this:
( c ) ✂
As it happens, this runs 30% slower on my machine, so whatever optimization tricks happened back then aren't in effect now. But there are other odd looping tricks out there. In particular, one that creates several variables, hoping to make more efficient use of the standard registers in compilation. Here's an example using 8 such variables:
( c ) ✂
No one would enjoy writing this code, but it does give you roughly a 80% speed increase. Interesting, if academic.
And then there are the various ways we could try to use the HPC routines in the Accelerate framework, either using fns in vDSP or in BLAS, though the BLAS one only helps us for the sum since there are no negative values, and we still need vDSP to help set up the problem. Here's an example of using vDSP:
( c ) ✂
and the other version is exactly as above, but swapping out the last two lines for:
( c )
I'm sure you noticed what a pain the setup is. I'm also making use of some in-line anonymous variable references to constants, &(double){ 1 }, which adds to the ugly, while slightly convenient. Why bother looking at the second two if it's such a mess, relatively? You may be walking into such a loop with everything sitting in array already, and the setup here would then go away. If the speed gains are big enough, you may be tempted to use these functions.
I was getting very different results for different array sizes, so ended up creating a shell script to go through a wide range across all the various techniques, including testing the middle solution for 2, 3, 4, 5, 6, 8 and 12 intermediate summing variables, just to test for a sweet spot. Wasn't as awful as it sounds. Here are the results, plotted lin-log:
Something that I forgot to make clear when I first posted this:
This is a graphing showing performance gain over naive looping. Higher scores are better.
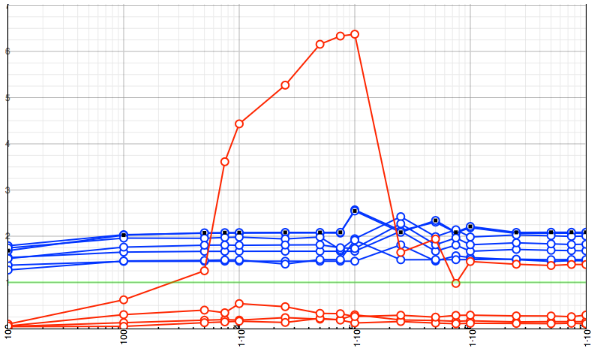
The green is the base benchmark of naive looping. The blue lines are the various attempts using intermediate summer variables. The red represent both Accelerate attempts (there are 4 of them because I wanted to check against including or not including the setup times).
So, clearly only one Accelerate version leaps out here, and it's the version that uses BLAS, but it's critical that it not include the setup in the timing, and only for certain array sizes. The vrampD fn seems to be very costly. But, if you already have your data in that form, one stands to gain a roughly 4-6x speed increase. Not insane, but nice, if the problem is already vectorized.
Back to the initial loop, however, which often is not vectorized. Interesting to see that the blue variations almost roughly double the speed. How many intermediate values was best overall? For my Xeon using the current clang compiler, the magic number was 5, though 4, 6 and 8 were roughly the same.
One more loop type before we go. 2-d C array in a nested loop. Consider the following:
( c ) ✂
now try swapping the loop order:
( c ) ✂
The second one is, on my machine, just over twice as fast. This has to do with the way that C addresses memory, it's quicker to stroll through nearby column data than to grab the same column data from different rows in succession. (There's an old PDF from 2005 dealing with PPC G5s that claimed a 30x difference in these loops. Nothing so dramatic happens here for whatever reason, though twice as fast is nothing to ignore.)
I haven't tested this stuff on A5 chips. That's for the reader. Just slightly interesting looping tests. And maybe, just maybe, of practical value when you need to squeeze out some performance.
( c ) ✂
1 for (i=0; i<ITERATIONS; i++)
2 sum += i;
where sum is a double and i is an integer. I had seen some old slides about compiling this on PPC machines that indicated that using a "ghost" double variable in the loop would triple the speed of the loop, so I had to try that on my Xeon. It goes something like this:
( c ) ✂
1 for (i=0, j=0.0; i<ITERATIONS; i++, j++)
2 sum += j;
As it happens, this runs 30% slower on my machine, so whatever optimization tricks happened back then aren't in effect now. But there are other odd looping tricks out there. In particular, one that creates several variables, hoping to make more efficient use of the standard registers in compilation. Here's an example using 8 such variables:
( c ) ✂
1 double sum0, sum1, sum2, sum3, sum4, sum5, sum6, sum7;
2 sum0 = sum1 = sum2 = sum3 = sum4 = sum5 = sum6 = sum7 = 0.0;
3
4 for (i = 0; (i+7)<ITERATIONS; i+=8) {
5 sum0 += i; sum1 += i + 1.0; sum2 += i + 2.0; sum3 += i + 3.0;
6 sum4 += i + 4.0; sum5 += i + 5.0; sum6 += i + 6.0; sum7 += i + 7.0;
7 }
No one would enjoy writing this code, but it does give you roughly a 80% speed increase. Interesting, if academic.
And then there are the various ways we could try to use the HPC routines in the Accelerate framework, either using fns in vDSP or in BLAS, though the BLAS one only helps us for the sum since there are no negative values, and we still need vDSP to help set up the problem. Here's an example of using vDSP:
( c ) ✂
1 double *vramp = (double *)malloc( ITERATIONS * sizeof( double ) );
2 double *vident = (double *)malloc( ITERATIONS * sizeof( double ) );
3 double *vout = (double *)malloc( ITERATIONS * sizeof( double ) );
4
5 catlasdset( ITERATIONS, 1, vident, 1 ); // set vident to all 1s
6 vDSPvrampD( &(double){ 0 }, &(double){ 1 }, vramp, 1, ITERATIONS); // vramp: 0, 1, 2, 3, 4, …
7 vDSPvrsumD( vramp, 1, vident, vout, 1, ITERATIONS ); // rolling sum, vout: 0, 1, 3, 7, 12, …
8
9 sum2 = vout[ITERATIONS-1];
and the other version is exactly as above, but swapping out the last two lines for:
( c )
1 sum2 = cblasdasum( ITERATIONS, vramp, 1 );
I'm sure you noticed what a pain the setup is. I'm also making use of some in-line anonymous variable references to constants, &(double){ 1 }, which adds to the ugly, while slightly convenient. Why bother looking at the second two if it's such a mess, relatively? You may be walking into such a loop with everything sitting in array already, and the setup here would then go away. If the speed gains are big enough, you may be tempted to use these functions.
I was getting very different results for different array sizes, so ended up creating a shell script to go through a wide range across all the various techniques, including testing the middle solution for 2, 3, 4, 5, 6, 8 and 12 intermediate summing variables, just to test for a sweet spot. Wasn't as awful as it sounds. Here are the results, plotted lin-log:
Something that I forgot to make clear when I first posted this:
This is a graphing showing performance gain over naive looping. Higher scores are better.

The green is the base benchmark of naive looping. The blue lines are the various attempts using intermediate summer variables. The red represent both Accelerate attempts (there are 4 of them because I wanted to check against including or not including the setup times).
So, clearly only one Accelerate version leaps out here, and it's the version that uses BLAS, but it's critical that it not include the setup in the timing, and only for certain array sizes. The vrampD fn seems to be very costly. But, if you already have your data in that form, one stands to gain a roughly 4-6x speed increase. Not insane, but nice, if the problem is already vectorized.
Back to the initial loop, however, which often is not vectorized. Interesting to see that the blue variations almost roughly double the speed. How many intermediate values was best overall? For my Xeon using the current clang compiler, the magic number was 5, though 4, 6 and 8 were roughly the same.
One more loop type before we go. 2-d C array in a nested loop. Consider the following:
( c ) ✂
1 double array2d[ROWS][COLS];
2
3 for (j=0; j<COLS; j++)
4 for (i=0; i<ROWS; i++)
5 sum1 += array2d[ i ][ j ];
now try swapping the loop order:
( c ) ✂
1 for (i=0; i<ROWS; i++)
2 for (j=0; j<COLS; j++)
3 sum2 += array2d[ i ][ j ];
The second one is, on my machine, just over twice as fast. This has to do with the way that C addresses memory, it's quicker to stroll through nearby column data than to grab the same column data from different rows in succession. (There's an old PDF from 2005 dealing with PPC G5s that claimed a 30x difference in these loops. Nothing so dramatic happens here for whatever reason, though twice as fast is nothing to ignore.)
I haven't tested this stuff on A5 chips. That's for the reader. Just slightly interesting looping tests. And maybe, just maybe, of practical value when you need to squeeze out some performance.